Rangkaian Logika Sequensial dan Kombinasional

1. Rangkaian logika sekuensial

     
     Outputnya tidak bergantung pada nilai input saat itu, tetapi juga input-input sebelumnya. Karena itu dikatakan mempunyai karakteristik memori.

Piranti sekuensial :

• Flip-flop

      Flip-Flop merupakan sirkuit elektronik yang memiliki dua arus stabil dan dapat digunakan untuk menyimpan informasi. Sebuah flip-flop merupakan multivibrator-dwistabil. Sirkuit dapat dibuat untuk mengubah arus dengan sinyal yang dimasukkan pada satu atau lebih input kontrol dan akan memiliki satu atau dua output.

Flip-flop dapat dibagi dalam beberapa jenis umum: 

1. SR ("set-reset")
2. D ("data" atau "delay")
3. T ("toggle")
4. JK

• Register

Fungsi : sebagai memori sementara untuk penggeseran data ke kiri atau ke kanan.

   Dibangun dari kumpulan flip-flop, banyaknya flip-flop menentukan panjang register dan juga panjang kata biner yang dapat disimpan di dalam register.

• Register seri

Contoh :  Register seri geser ke kanan 4 bit

Diagram Logika :

• Register Paralel

Contoh : Register paralel geser ke kanan yang beresirkulasi 4 bit.

Diagram logika :

• Counter

     Merupakan rangkaian logika pengurut yang membutuhkan karakteristik memori dan sangat ditentukan oleh pewaktu. Disusun dari sejumlah flip-flop. 

Karakteristik utamanya :

1. Jumlah hitungan maksimum (modulus pencacah)
2. Menghitung ke atas (up counter) atau ke bawah (down counter).
3. Operasi sinkron (serempak, pencacah paralel) atau asinkron (seri, pencacah gelombang).

Contoh : Pencacah gelombang 4 bit (modulo-16), menghitung ke atas.

Diagram logika : 

Tabel kebenaran :

Berdasarkan waktu sinyal, dapat dibedakan menjadi :

• Rangkaian sekuensial sinkron :

    Operasinya disinkronkan dengan pulsa waktu yang dihasilkan oleh pembangkit pulsa yang merupakan masukan bagi rangkaian. Sehingga keluaran akan berubah hanya setiap adanya masukan pulsa waktu, meskipun inputnya tidak berubah.

• Rangkaian sekuensial asinkron :

         Operasinya hanya bergantung pada input, dan dapat dipengaruhi setiap waktu.

     2.  Rangkaian logika kombinasional

          Rangkaian yang outputnya bergantung pada keadaan nilai input pada saat itu saja.

Piranti kombinasional : 

• Rangkaian gerbang OR-AND–NOT

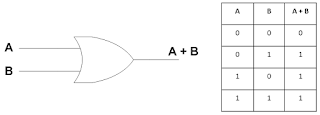
     1. OR

      Suatu rangkaian logika yang mempunyai beberapa jalan masuk (Input) dan hanya mempunyai satu jalan keluar (Output).

     2. AND

       Suatu rangkaian logika yang mempunyai beberapa jalan masuk (Input) dan hanya mempunyai satu jalan keluar (Output).

     3. NOT

      Suatu rangkain logika yang berfungsi sebagai “Pembalik”. Bila pada rangkain ini dimasukkan konstante “1” (Input) maka keluarannya (Output) adalah konstante “0”. Atau bila dimasukkan variabel A, maka keluarannya adalah A’, demikian juga sebaliknya.

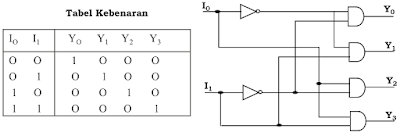
• Decoder

       Rangkaian kombinasi yang akan memilih salah satu keluaran sesuai dengan konfigurasi input. Decoder memiliki n input dan 2n output.

        Untuk merancang rangkaian kombinasional dapat digunakan Decoder dan eksternal OR gate (rangkaian kombinasi n - input dan  m – output dapat diimplementasikan dengan n to 2n line decoder dan m – OR gate).

• Adder

        Manipulasi matematika seperti menjumlah,mengurang,mengali dan membagi dapat dilakukan dengan logika penjumlahan.

                                                                                   Gambar Rangkaian Logika :                                  

Persamaan Output (Metode Minterm)  

S   = A’B’Cin + ABCin’ + AB’Cin’ + ABCin 

     = A’ (B’Cin + BCin’) + A (B’Cin’ + BCin)

     = A’ (B Å Cin) + A (B Å Cin)’

     = A Å B Å Cin

Co = A’BCin + AB’Cin + ABCin’ +ABCin

     = Cin (A’B + AB’) + AB (Cin’ + Cin)

     = Cin (A Å B) + AB

• Subtractor

        Untuk memahami azas – azas rangkaian pengurang (subtractor) kita ikuti aturan pengurangan biner sebagai berikut :

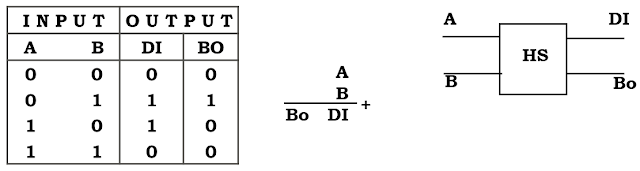
Half Subtractor (HS).

A – B = D (Difference).   B (Borrow)

0 – 0 = 0

0 – 1 = 1        Borrow 1

1 – 0 = 1

1 – 1 = 0 

     Tabel Kebenaran:                                                                                Simbol Half Subtractor (HS) :

                                                                                   Gambar Rangkaian Logika :                                  

                                                                           Persamaan output :

Untuk DI = A’B + A’B = A + B

        Bo = A’ B

• Multiplexer (MUX)

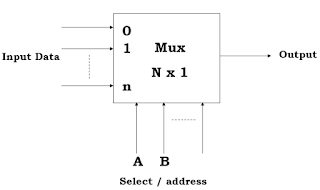  Rangkaian logika yang menerima beberapa input data digital dan menyeleksi salah satu dari input tersebut pada saat tertentu, untuk dikeluarkan pada sisi output.

    Seleksi data-data input dilakukan oleh selector line, yang juga merupakan input dari multiplexer tersebut. 

Contoh :

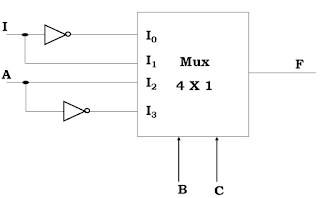
             F(ABC) = Σ1, 3, 5, 6

             Mux (4x 1)

                                                                                         Input Variabel A diambil sebagai data                                                                                                        sedangkan B dan C sebagai address.

Gambar Rangkaian Logika :